DataStructures-Algorithms

动态规划

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

背包问题总结

背包问题 (Knapsack problem x ) 有很多种版本，常见的是以下三种：

• 0-1 背包问题 (0-1 knapsack problem)：每种物品只有一个
• 完全背包问题 (UKP, unbounded knapsack problem)：每种物品都有无限个可用
• 多重背包问题 (BKP, bounded knapsack problem)：第 i 种物品有 n[i] 个可用

  0-1背包问题

  0-1背包中一种物体只有一个，放入数量为0或者1
  定义状态 dp[i][W]，表示“把前 i 种物品装进重量限制为 W 的背包可以获得的最大价值”
  v[i]表示物品i的价值，w[i]表示物品i的重量，W 为背包的重量限制
  若只考虑第i件物品的策略（放或不放），那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为W的背包中”，价值为f[i-1][W]；如果放第i件物品，那么问题就转化为“前i-1
  件物品放入剩下的容量为W-w[i]的背包中”，此时能获得的最大价值就是f[i-1][W-w[i]]再加上通过放入第i件物品获得的价值v[i]
  0/1背包问题状态转移方程便是：

     dp[i][W] = max{dp[i − 1][W],  dp[i − 1][W − w[i]] + v[i]}

  优化空间复杂度

  以上方法的时间和空间复杂度均为O(n*W)，其中时间复杂度基本已经不能再优化了，但空间复杂度却可以优化到O(W):
  dp[i][W]只与dp[i-1][W]和dp[i-1][W-w[i]]有关，即只和i-1时刻状态有关，所以我们只需要用一维数组d[]来保存i-1时的状态d[]。
  假设i-1时刻的d[]为{a0，a1，a2，…，aW}，那么i时刻的d[]中第W个应该为max(aW,aW-w[i]+v[i])即max(d[W],d[W-w[i]]+v[i])，
  这就需要我们遍历W时逆序遍历，这样才能保证求i时刻d[W]时d[W-w[i]]是i-1时刻的值。如果正序遍历则当求d[W]时
  其前面的d[0],d[1]，…，d[W-1]都已经改变过，里面存的都不是i-1时刻的值，这样求d[W]时利用d[W-w[i]]必定是错的值。最后d[W]即为最大价值

    d[W]=max{d[W],d[W-w[i]]+v[i]};

  注意：遍历W时务必从右到左，因为d[W]只依赖于上一阶段的结果，从右到左避免覆盖上阶段有用结果

完全背包问题

完全背包中每种物品都˚有无限个，可以放满背包为止
完全背包问题状态转移方程是：

   dp[i][W] = max{dp[i − 1][W],  dp[i][W − w[i]] + v[i]}

两项分别代表物品i不选择或者选择，由于对物品i没有限制，故后一项为dp[i]而非上面的dp[i-1]
 
或用以下递推式（上面的效率要高一点）：

p[i][W] = max( dp[i-1][W-k*w[i]] + k*v[i] ),   k为选择物品的个数， k=0,1,2...W/w[i] (0 ≤ k ∗ w[i] ≤ W)

基于前i-1个物品，在选择不同个数的物品i的方案中选择最大的那个
 
可以简化为：

   d[W] = max{d[W], d[W-k*w[i]] + k*v[i]}

注意：遍历W时务必从右到左，原因同上

多重背包问题

有n种物品和一个重量限制为 W的背包。第i种物品最多有n[i]件可用，每件重量是w[i]，价值是v[i]。求这些物品装进重量限制为 W 的背包可以获得的最大价值。
这里又多了一个限制条件，每个物品规定了可用的次数。
多重背包问题状态转移方程是：（注意：范围限制）

dp[i][W] = max(dp[i−1][W−k∗w[i]] + k∗v[i] ),   k为选择物品的个数，   0 ≤ k ≤ n[i],0 ≤ k ∗ w[i] ≤ W

n[i]为物品i限制的个数
基于前i-1个物品，在选择不同个数的物品i的方案中选择最大的那个
 
可以简化为：

   d[W] = max{d[W], d[W-k*w[i]] + k*v[i]}

注意：遍历W时务必从右到左，原因同上

树

树的深度优先遍历、广度优先遍历

对于树形结构主要有两种遍历方式：深度优先遍历和广度优先遍历。
一个简单的树结构图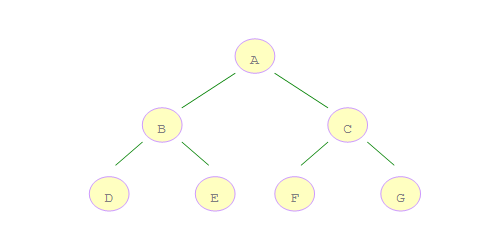

深度优先遍历

对于一颗二叉树，深度优先搜索(Depth First Search)是从根节点开始沿着树的深度遍历树的节点，尽可能深的搜索树的分支。上图的深度优先遍历结果为：ABDECFG
深度优先遍历的特点是，从树的根节点开始，先遍历左子树，然后遍历右子树。因此我们可以利用堆栈的先进后出的特点，现将右子树压栈，再将左子树压栈，这样左子树就位于栈顶，可以保证结点的左子树先于右子树被遍历。
我们借助栈结构来实现深度优先遍历，代码如下：

Stack<Node> stack = new Stack<Node>();
List<Node> result = new ArrayList<Node>();
stack.push(root);
while (!stack.isEmpty()) {
	Node top = stack.pop();
	result.add(top);
	List<Node> children = top.getChildren();
	if (children != null && children.size() > 0) {
		for (int i = children.size() - 1; i >= 0; i--) {
			stack.push(children.get(i));
		}
	}
}

广度优先遍历（层序遍历）

对于一颗二叉树，广度优先搜索（Breadth First Search）是从根节点开始沿着树的宽度依次遍历树的每个节点。上图的遍历结果为：ABCDEFG
如上图所示的二叉树，A 是第一个访问的，然后顺序是 B、C，然后再是 D、E、F、G。
那么，怎样才能来保证这个访问的顺序呢？
借助队列数据结构，由于队列是先进先出的顺序，因此可以先将左子树入队，然后再将右子树入队。这样一来，左子树结点就存在队头，可以先被访问到。
我们借助队列结构来实现树的广度优先遍历，代码如下：

Queue<Node> queue = new LinkedBlockingQueue<Node>();
List<Node> result = new ArrayList<Node>();
queue.add(root);
while (!queue.isEmpty()) {
	Node first = queue.poll();
	result.add(first);
	List<Node> children = first.getChildren();
	if (children != null && children.size() > 0) {
		for (int i = 0; i < children.size(); i++) {
			queue.add(children.get(i));
		}
	}
}

字典树

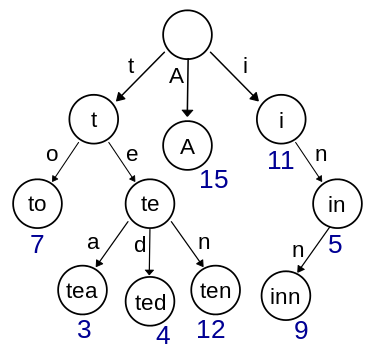
字典树主要有如下三点性质：

1. 根节点不包含字符，除根节点意外每个节点只包含一个字符。
2. 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
3. 每个节点的所有子节点包含的字符串不相同。

   八大排序

   快速排序的思想

   在数组中找到一个基准数（pivot）
   分区，将数组中比基准数大的放到它的右边，比基准数小的放到它的左边
   继续对左右区间重复第二步，直到各个区间只有一个数，这时候，数组也就有序了。

   快速排序算法是不稳定的算法

   27 23 27 3
   以第一个27作为pivot中心点，则27与后面那个3交换，形成
   3 23 27 27，排序经过一次结束，但最后那个27在排序之初先于初始位置3那个27，所以不稳定。

   堆排序的思想

   利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。
   其基本思想为(大顶堆)：
4. 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无须区；
5. 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
6. 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

   链表

   单向链表、双向链表、双向循环链表

   单向链表：必须从头节点开始遍历， 只能访问后继
   双向链表：可以顺序访问外,还可以逆推， 可以同时访问前驱后继
   双向循环链表：双向循环链表在内存分配上更容易管理,因为它可以重复利用已分配的内存.可以看出一个圆